1. 데이터 정의_ 공부한 시간에 따른 결과 점수 예측
| 시간(x) | 포인트(y) |
| 1 | 2 |
| 2 | 4 |
| 삼 | 6 |
| 4 | ? |
- x_train = torch.FloatTensor(((1),(2),(3)))
- y_train = torch.FloatTensor(((2),(4),(6)))
2. 가설
| y = Wx + b |
가중치와 편향을 0으로 초기화합니다.
require_grad=True : 학습할 것임을 지정
- W = torch.zeros(1, requires_grad=True)
- b = torch.zeros(1, requires_grad=True)
- 가설 = x_train * W + b
3. 손실 계산
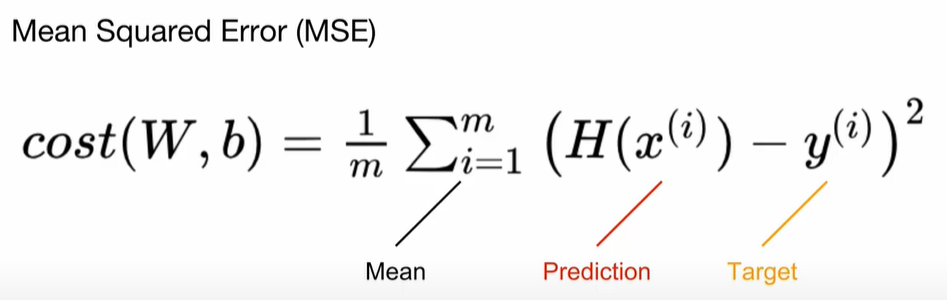
평균(torch.mean 포함)
- 비용 = torch.mean((가설 – y_train) ** 2)
모두를 위한 딥러닝 시즌 2_PyTorch
4.경사 하강법
torch.optim 라이브러리를 사용하십시오.
(W,b)는 학습할 텐서입니다. lr = 0.01 은 학습률
- 옵티마이저 = optim.SGD((W, b), lr=0.01)
- 옵티마이저.zero_grad()
비용.역방향()
옵티마이저.스텝()
1. zero_grad()로 그래디언트 초기화
2. backward()로 기울기를 계산합니다.
3. step() 개선
# 데이터
x_train = torch.FloatTensor(((1), (2), (3)))
y_train = torch.FloatTensor(((1), (2), (3)))
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정, 학습준비
optimizer = optim.SGD((W, b), lr=0.01)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W + b
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()다변수 선형 회귀
1.데이터
| 퀴즈1(x1) | 퀴즈2(x2) | 퀴즈3(x3) | 끝(y) |
| 73 | 80 | 75 | 152 |
| 93 | 88 | 93 | 185 |
| 89 | 91 | 80 | 180 |
| 96 | 98 | 100 | 196 |
| 73 | 66 | 70 | 142 |
- x1_train = torch.FloatTensor(((73), (93), (89), (96), (73)))
- x2_train = torch.FloatTensor(((80), (88), (91), (98), (66)))
- x3_train = torch.FloatTensor(((75), (93), (90), (100), (70)))
- y_train = torch.FloatTensor(((152), (185), (180), (196), (142)))
2. 가설 기능

- 가설 = x_train.matmul(W) + b
계산은 matmul로 한 번에 할 수 있습니다.
3. 비용
비용 = torch.mean((가설 – y_train) ** 2)
4. torch.optim을 사용한 경사하강법

- 옵티마이저 = optim.SGD((W, b), lr=1e-5)
- 옵티마이저.zero_grad()
비용.역방향()
옵티마이저.스텝()
x_train = torch.FloatTensor(((73, 80, 75),
(93, 88, 93),
(89, 91, 90),
(96, 98, 100),
(73, 66, 70)))
y_train = torch.FloatTensor(((152), (185), (180), (196), (142)))
# 모델 초기화
W = torch.zeros((3, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD((W, b), lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train.matmul(W) + b # or .mm or @
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
print('Epoch {:4d}/{} hypothesis: {} Cost: {:.6f}'.format(
epoch, nb_epochs, hypothesis.squeeze().detach(), cost.item()
))Pytorch 클래스를 사용한 경사 하강법
nn.모듈
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1)
def forward(self, x):
return self.linear(x)- nn.module을 상속하여 모델을 생성합니다.
- nn.module(3,1) : 입력 차원 = 3, 출력 차원 = 1
- 가설 계산은 forward()에서 수행됩니다.
- 기울기 계산은 Pytorch에 의해 수행됩니다. 뒤로()
F.mse_loss
import torch.nn.functional as F
cost = F.mse_loss(prediction, y_train)손쉬운 손실 변경
x_train = torch.FloatTensor(((73, 80, 75),
(93, 88, 93),
(89, 91, 90),
(96, 98, 100),
(73, 66, 70)))
y_train = torch.FloatTensor(((152), (185), (180), (196), (142)))
# 모델 초기화
model = MultivariateLinearRegressionModel()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1e-5)
nb_epochs = 20
for epoch in range(nb_epochs+1):
# H(x) 계산
hypothesis = model(x_train)
# cost 계산
cost = F.mse_loss(hypothesis, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
